はじめに
こんにちは、データサイエンティストの本多です。久々にエンジニアブログに投稿します。
今回は各企業の(新卒の)採用力や各大学の就職力を社内のデータから指標化することを試みました。ただ、始めに断っておくと、結果はあまり上手くいっていません。良い結果が出ていたら働きがい研究所で発表できたのですが、かと言ってこのままお蔵入りさせるのももったいないので、試した内容をブログのネタにします。 へぇ〜こんなこともやっているんだ、くらいの気持ちで読んでください。また、自分ならもっと上手くできるという方の応募も絶賛お待ちしています。
企業の採用力を指標化したい
オープンワークでは企業に対してリクルーティングのサービスも提供しています。そして、そのキャッチフレーズが『社員の「働きがい」を採用力に』です。
ここで言う「採用力」とは何でしょうか。
もちろん、「働きがい」の方も奥の深いテーマでこれを計測する完全な指標はありません。それでも、OpenWorkの総合評価のアルゴリズムは検討を重ねてきており、 働きがい研究所では別視点でのスコア化を試みてランキング化するなどの取り組みを続けています。 その一方で「採用力」はまだ検証が進んでいません。総合評価が高いと、求人の閲覧数や応募ボタンのクリック率、スカウトへの返信率等が高い傾向にあることはわかっており、採用において総合評価が高い企業は有利らしいことがわかっているだけという状況です。
できればこの「採用力」も何らかの形で指標化したいと思っています。
そして、総合評価が0.1点上がると採用力は平均何ポイント上がりますと具体的に示したい。また、各企業が組織文化や採用手法の改善に取り組まれた時には、その結果御社の採用力は何ポイント上がりました、と教えてあげられるようになりたいです。そのためにも、「採用力」を指標化するニーズはあります。
採用に関しては新卒採用と中途採用で大きく傾向が違います。それぞれ同じような手法を試してみましたが、この記事では大卒者の新卒採用に絞って紹介します。
先行事例と今回の目標
さて、世の中には「採用力」に近いものをランキング化している例は多数あります。例えば、大学生にアンケートを取った就職人気ランキングなどがそれです。また、その中にはOpenWork内部での検索データを元にした就職注目企業ランキングなど、僕たちが発表したものもあります。
就活生に対して認知度を上げ、応募者を増やすことは採用を成功させるために必要なことなのでこれらももちろん重要な指標です。特に多くの人数を採用する必要のある企業にとっては必須とも言えます。
しかし、今回は人気や知名度ではなく、実際に入社したことを基準にしたいと考えました。実はこれにも先行事例はあります。例えば、有名大学を数校ピックアップし、それらの大学の卒業生を何人採用しているかで評価する方法などがあります。ただし、この方法には対象大学の選定に恣意性が残ります。また、対象に含まれない大学からの採用は評価されないこと、その一方で対象大学を全部一律に同じ重みで評価することなども課題です。これらの点を改善してより客観的な指標で、企業の採用力をうまく定義できないかなと考えました。
使用するデータについて
オープンワークで何か新しいスコアやランキングを作る場合、通常は会社評価レポートのデータを使います。でも、その中には、新卒入社/中途入社の区分はありますが、投稿者がどこの大学の出身者なのかはわかりません。そのため、かつてのオープンワークでは出身大学と就職先のデータをなかなか集められない状況にありました。
しかし、先述のリクルーティングサービスの開始により、Web履歴書のデータが蓄積されるようになったことで、状況が大きく変わりました。Web履歴書には出身大学と就職先企業が合わせて記録されており、現在ではそのデータも数万件規模になりました。 そこで、今回はこちらを使うことにしました。
準備として直近3年間の間に大学を卒業して就職した人のデータを抽出し、出身大学と新卒就職先の企業名の一覧を作成しておきます。(表記ゆれ等があるので、この作業も地味に大変でした。)
仮定とその数式化
用意したWeb履歴書のデータから企業の採用力と大学の就職力の指標化を目指すにあたって、試しに次のように仮定してみました。
まず前提として、企業ごとに「採用力」というスコアがあり、大学ごとに「就職力」というスコアがあるとします。(もちろん、同じ企業であっても職種によって違いはありますし、同じ大学によっても学部によって就職状況は全く違いますが、まずは、企業/大学単位の指標化を目指しました。)
そして、ここで定義した「採用力」と「就職力」には次の関係が成り立つとします。
- 就職力が高い大学の学生を多く採用できている企業は採用力が高い。
- 採用力が高い企業に多くの学生が就職している大学は就職力が高い。
この2つはある程度同意を得やすい仮定なのではないでしょうか。これを言い換えると次のようになります。勘のいい人はこの辺りで特異ベクトルだと気付くかもしれませんね。
- 企業の採用力は、採用元の各大学について「各大学からその企業に就職した人数×各大学の就職力」 を合計した値に比例する。
- 大学の就職力は、就職先の各企業について「その大学から各企業に就職した人数×各企業の採用力」 を合計した値に比例する。
文章だとこの先不便なので、数式化します。企業と大学にそれぞれインデックスを振り、企業i $(i=0, 1, \dots ,m-1)$の採用力を$c_i$、大学j $(j=0, 1, \dots ,n-1)$の就職力を$s_j$と表します。 そしてそれをまとめたベクトル、$\mathbf{c}$と$\mathbf{s}$を定義します。
$$\mathbf{c} = (c_0, c_1, \dots, c_n)^{\top}$$ $$\mathbf{s} = (s_0, s_1, \dots, s_m)^{\top}$$
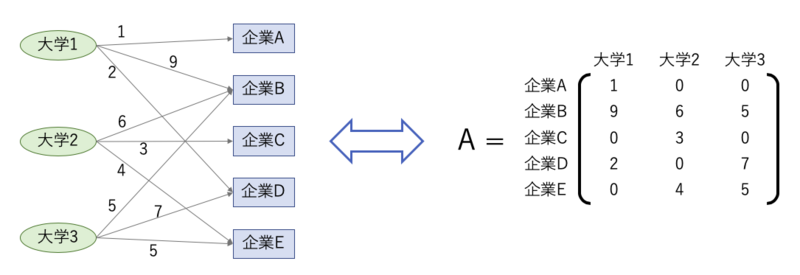
更に、各大学から各企業への就職人数は$i,j$成分が、企業iの大学jからの採用人数で定義される$m\times n$行列$\mathbf{A}$で表現しておきます。
すると、 先程の仮定は次の式で表せます。($\propto$は比例の意味です。) $$ \begin{align} \mathbf{c} & \propto A \mathbf{s}\\ \mathbf{s} & \propto A^{\top} \mathbf{c} \end{align} $$
実際に計算してみる
さて、定式化ができましたが、この式には一つ困ったことがあります。大学の就職力を算出するには企業の採用力が必要で、企業の採用力を算出するには大学の就職力が必要なことです。
このままでは進まないので、まずは大学の就職力を全部等しく「1」だと仮定してスタートしましょう。すると、$\mathbf{c} = A \mathbf{s}$ から、企業の採用力が計算できます。それを使って、$\mathbf{s} = A^{\top} \mathbf{c}$から再び大学の就職力が計算できます。 これを繰り返すと、 就職力と採用力はどちらもどこまでも大きな値になってしまいます。
そこで、この2つを計算したら、ベクトル$\mathbf{c},\mathbf{s}$がそれぞれ長さ1になるように長さで割って正規化することにしましょう。 結果的に次の手順で計算することになります。
- 各大学の就職力を1とおく。
- $\mathbf{c} = A \mathbf{s}$ の式から、企業の採用力を計算する。
- $\mathbf{s} = A^{\top} \mathbf{c}$ の式から大学の就職力を計算する。
- 企業の採用力ベクトル$\mathbf{c}$と大学の就職力ベクトル$\mathbf{s}$を長さ1に正規化する。
- 2~4を繰り返す。
これを実際にやってみると、$\mathbf{c}$と$\mathbf{s}$はそれぞれ特定のベクトルに収束します。
収束先の値についての線形代数的な説明
さて、前節の計算で就職力と採用力のベクトルが一定の値に求まる事がわかります。 この収束先が気になりますが、実はこれは行列$\mathbf{A}$の絶対値が最大の特異値に対する特異ベクトルになります。 就職力のほうが右特異ベクトルで、採用力のほうが左特異ベクトルです。
もう少し説明します。 先程の行列$\mathbf{A}$を、 $m\times m$の直交行列$\mathbf{U}$と、$n\times n$の直交行列$\mathbf{V}$、 さらに、非対角成分が0の$m\times n$行列 $\mathbf{S}$を用いて $$ \mathbf{A} = \mathbf{USV^{\top}} $$ と特異値分解したとします。
この時、行列$\mathbf{S}$の対角成分が絶対が大きい順に並んでいるとすると、直交行列 $\mathbf{U}=[\mathbf{u}_0, \mathbf{u}_1, \dots, \mathbf{u}_{m-1}]$の一番左の列ベクトル$\mathbf{u}_0$が、 各企業の採用力のベクトルになり、直交行列 $\mathbf{V}=[\mathbf{v}_0, \mathbf{v}_1, \dots, \mathbf{v}_{n-1}]$の一番左の列ベクトル$\mathbf{v}_0$が、各大学の就職力のベクトルになります。
これを使えばループを回して収束を待たなくても、簡単に計算できます。
元ネタについて
この就職データの行列を特異値分解して指標として使うアイデアには元ネタがあります。 SEOを担当されている方はご存知だと思いますが、HITSアルゴリズムというWebページを評価する手法があります。これは各ページにリンク集としての便利さを示すHub Scoreと、そのページがどれだけリンクされているかを示すAuthority Score の2つのスコアを定義し、算出するものです。
Hub Scoreが高いページからリンクされているほど Authority Score は高くなり、Authority Score が高いページへリンクするほどHub Scoreは高くなります。最初の採用力と就職力の仮定と同じですね。細かく言うと、HITSアルゴリズムはリンクしてるかどうかを示す0と1の行列を使い、この記事で書いている採用力と就職力は就職した人数で重み付けしている点が違います。
算出した結果を検証する
ここまでの計算により、大学・企業別の就職人数の行列から、各企業と各大学に対して、一定の値を得ることができました。さて、ここで気になるのが「算出された値は採用力と就職力を表す指標としてどの程度信用できるのか」ということです。この問が非常に重要です。良い点悪い点あるので、順番に説明します。
良かったところ
まず前提として、ここで算出した採用力と就職力(と呼んでいる値)は、最初に仮定した次の2つの性質を完全に満たします。
- 就職力が高い大学の学生を多く採用できている企業は採用力が高い。
- 採用力が高い企業に多くの学生が就職している大学は就職力が高い。
しかも、それぞれ値が大きい順に並べてみると、大学の方は有名大学が順番に登場し企業の方も大手有名企業ばかりが並びます。 仮定から明らかなのですが、ここで出した値はデータ件数が多い企業や大学ほど高い値が付いている傾向はあります。この点は、それぞれの値を人数で割って正規化し、「一人あたり」に変換することである程度補正できそうです。
計算に特異値分解を使ったメリットとして、企業や大学のユークリッド空間への埋め込みが同時に得られているのも良い点です。$\mathbf{u}_0$や$\mathbf{v}_0$以外の列ベクトルにも各企業や各大学の情報は反映されているので、機械学習の特徴量として使うなど別の目的でも活用の場面がありそうです。
明らかになった課題
さて、良い点だけ見れば成功したように見えるのですが、深刻な問題があることもわかりました。社外の事例やデータも含めて比較検証すると、明らかに採用力が高そうな会社(学生に人気があり、採用人数が多く、OpenWorkの総合評価も高い会社)の一部はスコアが不自然に低いのです。また、よく見ると最上位に並ぶ企業群は離職率が高めの会社が中心になっています。
この現象は利用したデータに起因します。僕たちにとってはいつものことですが、「分析対象がOpenWorkのデータである」ことは常に考慮する必要があります。今使っているデータは世の中の全就職者のデータではなく、最近3年間以内に就職して、OpenWorkにWeb履歴書を登録したユーザーのデータです。Web履歴書記入者の全員が転職希望者や経験者というわけではないのですが、それでも入社後早期に転職を考えている人のデータが中心になるというバイアスがあります。 そのため、実質的には「高学歴な新入社員がすぐに転職を考える企業ランキング」が出来上がってしまっていたわけです。これはこれで何かしら役に立ちそうではありますが、求めたかった指標とは全く違いますね。(このようなランキングなので、結果はこの記事でも非公開にさせていただきます。すみません。)
これまでに何度も分析してきた会社評価レポートのデータに関しては、このようなバイアスへの対応方法のナレッジもある程度溜まっていますが、蓄積され始めて日が浅く、まだ十分に分析できていないWeb履歴書データはまだまだ手探りで慎重に扱っていく必要があります。
改善に向けた取り組み
さて、検証の結果、この単純なアプローチでは採用力は上手く測れていない事がわかりました。しかし改善方法が考えられないわけではありません。
データのバイアスへの対応としては実は直近の就職者の履歴書ではなく、もっと昔のデータを使うことも有効です。じつは10年くらいの前の就職者のデータを使って同じことを計算するだけでも、長期的に勤務している人のデータも入ってくるため、かなり改善します。ただ、今更10年前の採用力を評価できても実用性が低いのが難しいところです。
Web履歴書データを使うこと自体が課題であれば、他のデータを使うことも考えられます。実は昨年から就活を終えた学生ユーザーに対して入社予定先の企業を教えてもらうなどの取り組みもはじめており、このデータも今後蓄積していけば活用できるものになりそうです。そしてもちろん、サービスで蓄積できたデータだけでなく、社外のデータも収集して活用する事も考えられます。また、Web履歴書のデータを活用するとしても、全てを均等に扱うのではなく、入社後の定着状況や転職意欲なども考慮する方法もありそうです。
当然ですが、データを見直すだけでなく、算出方法にも改善の余地は多くあります。そもそも最初の仮定が職種も学部も考慮していない大雑把なものなので、そこから見直したほうが良いでしょう。また、特定の大学が有利になる傾向が見つかっていたり、データ件数と結果の信頼性の関係がまだ不明確であるなど、この他の課題も多数あるので、もし対外的に発表するのであればそれらの課題も解決する必要があります。
データサイエンティストの仕事の範囲
データサイエンティストの仕事の一つとして、データから新しいスコアやランキングを作ることもあることを話すと、機械学習やこの記事の特異値分解のあたりのような数学的な手法の部分がイメージされがちです。しかし、実際はもっと広い範囲に関わります。
この記事で言えば「企業の採用力を指標化したい」という課題設定の部分から始まり、「算出できた結果を検証する」フェーズまで含めて「データサイエンス」です。そして実際、指標やランキングの算出そのものより、その結果の検証のほうが多くの時間がかかります。(そのため、働きがい研究所用の集計や各メディアさんからの企画対応は算出にかかる時間だけ考えて納期設定すると大失敗する。)
成功事例を取り上げてこの仕事のことを説明しようとしても、どうしても「特異値分解を使って計算できました。めでたしめでたし。」になってしまい、最後の検証フェーズの存在とその重要性が伝わらないので、今回の記事には失敗事例を持ってきました。多くのデータを用意し、妥当そうな仮定を立て、(他分野で)実績のあるアルゴリズムを使い、一見それらしい結果が得られた。しかし詳しく検証したらこの結果はおかしい、となることもよくあるのです。
まとめ
今回の例ではデータとしてはWeb履歴書の卒業大学名と新卒入社した企業名のみを扱いました。失敗事例を持ってきてこんな事を言うのも恐縮ですが、この限られたデータでも扱い方しだいで何かしら面白い情報を見い出せそうだという可能性を感じていただけたらと思います。それに加えてWeb履歴書に限っても、卒業した大学名と企業名に限らず色々なデータが含まれています。また、僕たちが構築しているワーキングデータプラットフォームにはWeb履歴書以外にも多くのデータが存在し、その中にはもちろん企業クチコミデータもあります。しかし、これらのデータを分析し、活用する体制はまだ十分ではありません。せっかく集めているのに、ほとんど活用できていないデータもたくさんあります。
蓄積されたデータを活用してサービスをより良いものにしていくために、オープンワーク株式会社では一緒に働く仲間を募集しています。ミッションに共感し、データに興味をお持ちの方がいらっしゃいましたら、一緒に働いてみませんか。 vorkers.jp vorkers.jp